1. Тело брошено с поверхности земли под углом a к горизонту со скоростью V0. Каков максимальный радиус кривизны его траектории во время полета? Сопротивлением воздуха пренебречь, ускорение свободного падения равно g.
2. Материальная точка движется по плоскости,
начиная с момента времени t = 0, по закону: х = а соs ![]() t, у = b
sin
t, у = b
sin ![]() t.
Найти ускорение точки в момент первого
пересечения ею оси У.
t.
Найти ускорение точки в момент первого
пересечения ею оси У.
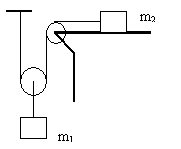 3. В системе,
изображенной на рисунке, массы тел равны m1
и m2. Трения нет, массы блоков и нити
пренебрежимо малы, участки нити, не лежащие на
блоках, вертикальны или горизонтальны. Найти
ускорение тела m1. Ускорение свободного
падения равно g.
3. В системе,
изображенной на рисунке, массы тел равны m1
и m2. Трения нет, массы блоков и нити
пренебрежимо малы, участки нити, не лежащие на
блоках, вертикальны или горизонтальны. Найти
ускорение тела m1. Ускорение свободного
падения равно g.
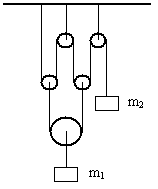 4. Найти ускорение массы m1
в системе, изображенной на рисунке. Нити невесомы
и нерастяжимы, блоки невесомы, трение в осях
блоков и о воздух отсутствует. Ускорение
свободного падения равно g.
4. Найти ускорение массы m1
в системе, изображенной на рисунке. Нити невесомы
и нерастяжимы, блоки невесомы, трение в осях
блоков и о воздух отсутствует. Ускорение
свободного падения равно g.
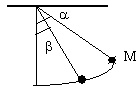 5. Маятник, состоящий из
маленького груза массы М, висящего на невесомой
нерастяжимой нити, отклоняют на угол
5. Маятник, состоящий из
маленького груза массы М, висящего на невесомой
нерастяжимой нити, отклоняют на угол ![]() от положения равновесия и
отпускают. Найти натяжение нити в тот момент,
когда нить отклонена от положения равновесия на
угол
от положения равновесия и
отпускают. Найти натяжение нити в тот момент,
когда нить отклонена от положения равновесия на
угол ![]() <
< ![]() . Ускорение свободного
падения равно g.
. Ускорение свободного
падения равно g.
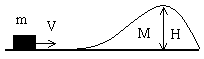 6. На гладкой
горизонтальной плоскости лежит небольшая шайба
массы m и гладкая горка массы М и высоты Н. Какую
минимальную скорость V надо сообщить шайбе, чтобы
она смогла преодолеть горку?
6. На гладкой
горизонтальной плоскости лежит небольшая шайба
массы m и гладкая горка массы М и высоты Н. Какую
минимальную скорость V надо сообщить шайбе, чтобы
она смогла преодолеть горку?
7. Два шарика с массами m1 и m2, движущиеся вдоль одной прямой со скоростями V1 и V2, испытывают упругое столкновение. Найти максимальное значение энергии упругой деформации шариков во время этого столкновения.
8. Ракета массы М, находящаяся в космосе вдали от
других тел, начинает ускоряться, выбрасывая из
двигателя с относительной скоростью U газы
массой ![]() в единицу
времени. Через сколько времени ракета достигнет
скорости V?
в единицу
времени. Через сколько времени ракета достигнет
скорости V?
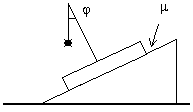 9. На тяжелой пластинке,
соскальзывающей с наклонной плоскости,
установлен отвес. Коэффициент трения между
пластинкой и плоскостью равен
9. На тяжелой пластинке,
соскальзывающей с наклонной плоскости,
установлен отвес. Коэффициент трения между
пластинкой и плоскостью равен ![]() . Определить угол отклонения
. Определить угол отклонения ![]() нити отвеса от
перпендикуляра к плоскости пластинки при
установившемся движении.
нити отвеса от
перпендикуляра к плоскости пластинки при
установившемся движении.
10. Горизонтальный диск вращают с постоянной
угловой скоростью ![]() = 6,0 рад/с вокруг вертикальной оси,
проходящей через его центр. По одному из
диаметров диска движется небольшое тело массы m =
0,50 кг с постоянной относительно диска скоростью
v = 50 см/с. Найти силу, с которой диск действует
на это тело в момент, когда оно находится на
расстоянии r = 30 см от оси вращения.
= 6,0 рад/с вокруг вертикальной оси,
проходящей через его центр. По одному из
диаметров диска движется небольшое тело массы m =
0,50 кг с постоянной относительно диска скоростью
v = 50 см/с. Найти силу, с которой диск действует
на это тело в момент, когда оно находится на
расстоянии r = 30 см от оси вращения.
11. Стержень пролетает с постоянной скоростью
мимо метки, неподвижной в К-системе отсчета.
Время пролета ![]() t = 20 нс - в
К-системе. В системе же отсчета, связанной со
стержнем, метка движется вдоль него в течение
t = 20 нс - в
К-системе. В системе же отсчета, связанной со
стержнем, метка движется вдоль него в течение ![]() t/ = 25 нс. Найти
собственную длину стержня.
t/ = 25 нс. Найти
собственную длину стержня.
12. Собственное время жизни некоторой
нестабильной частицы ![]() t0
= 10 нс. Найти путь, который пролетит эта частица до
распада в лабораторной системе отсчета, где ее
время жизни
t0
= 10 нс. Найти путь, который пролетит эта частица до
распада в лабораторной системе отсчета, где ее
время жизни ![]() t = 20 нс.
t = 20 нс.
13. Шарик массы m падает без начальной скорости с высоты h над поверхностью Земли. Найти модуль приращения вектора момента импульса шарика за время падения - относительно точки О системы отсчета, движущейся поступательно со скоростью V в горизонтальном направлении. В момент начала падения точка О совпадала с шариком. Сопротивление воздуха не учитывать.
14. На однородный сплошной цилиндр массы М и радиуса R намотана легкая нить, к концу которой прикреплено тело массы m. В момент t = 0 система пришла в движение. Пренебрегая трением в оси цилиндра, найти зависимость от времени:
а) угловой скорости цилиндра;
б) кинетической энергии всей системы.
15. Гладкий однородный стержень АВ массы М и
длины L свободно вращается с угловой скоростью ![]() 0
в горизонтальной плоскости вокруг неподвижной
оси, проходящей через его конец А. Из точки А
начинает скользить небольшая муфта массы m. Найти
скорость муфты относительно стержня в тот
момент, когда она достигнет его конца В.
0
в горизонтальной плоскости вокруг неподвижной
оси, проходящей через его конец А. Из точки А
начинает скользить небольшая муфта массы m. Найти
скорость муфты относительно стержня в тот
момент, когда она достигнет его конца В.
16. Однородный упругий прямоугольный брусок движется по гладкой горизонтальной плоскости под действием постоянной силы F, направленной вдоль бруска и равномерно распределенной по его торцу. Площадь торца равна S, модуль Юнга материала - Е. Найти относительную деформацию бруска в направлении действия данной силы.
17. Проволока длиной L натянута горизонтально
между двумя зажимами. К середине проволоки
подвешен груз весом Р, в результате чего возник
прогиб ![]() . Определить
зависимость
. Определить
зависимость ![]() от Р, если
известны модуль Юнга материала проволоки Е и ее
диаметр d. Считать начальное натяжение проволоки
малым,
от Р, если
известны модуль Юнга материала проволоки Е и ее
диаметр d. Считать начальное натяжение проволоки
малым, ![]() /L << 1.
/L << 1.
18. Какую работу необходимо совершить, чтобы, действуя постоянной силой на поршень, выдавить из горизонтально расположенного цилиндра через отверстие на его торце всю воду за время t? Начальный объем воды в цилиндре равен V, площадь сечения отверстия s много меньше площади поршня. Трение и вязкость пренебрежимо малы.
19. Свинцовый шарик равномерно падает в
глицерине, вязкость которого равна ![]() = 1,39 Па*с. При каком максимальном
диаметре шарика d его обтекание еще остается
ламинарным, если известно, что переход к
турбулентному обтеканию соответствует числу
Рейнольдса Rе = 0,5 (за характерный размер в
этом числе взят d)? Плотность глицерина
= 1,39 Па*с. При каком максимальном
диаметре шарика d его обтекание еще остается
ламинарным, если известно, что переход к
турбулентному обтеканию соответствует числу
Рейнольдса Rе = 0,5 (за характерный размер в
этом числе взят d)? Плотность глицерина ![]() 1 = 1,26 г/см3, плотность
свинца
1 = 1,26 г/см3, плотность
свинца ![]() 2 = 11,3 г/см3,
ускорение свободного падения g = 9,8 м/с2.
2 = 11,3 г/см3,
ускорение свободного падения g = 9,8 м/с2.
20. Сплошной однородный цилиндр массы М совершает малые колебания под действием двух пружин, общий коэффициент жесткости которых равен k (см. рис.). Найти период этих колебаний в отсутствии проскальзывания.
21.Найти логарифмический декремент затухания математического маятника длины L = 50 см, если за промежуток времени t = 5 мин. Его полная механическая энергия уменьшилась в n = 4*104 раз. Ускорение свободного падения g = 9,8 м/с2.
22. При частотах вынуждающей гармонической силы ![]() 1
и
1
и ![]() 2
амплитуда скорости частицы равна половине
максимального значения. Найти резонансную
частоту
2
амплитуда скорости частицы равна половине
максимального значения. Найти резонансную
частоту ![]() 0.
0.
23. На пути плоской звуковой волны,
распространяющейся в воздухе (плотность ![]() = 1,3 кг/м3), находится шар
радиусом R = 50 см. Длина волны звука
= 1,3 кг/м3), находится шар
радиусом R = 50 см. Длина волны звука ![]() = 20 см, частота
= 20 см, частота ![]() = 1700 Гц, амплитуда колебаний давления
= 1700 Гц, амплитуда колебаний давления ![]() p = 3,5 Па. Найти средний за
период колебаний поток энергии, падающий на шар.
p = 3,5 Па. Найти средний за
период колебаний поток энергии, падающий на шар.
24. Неподвижный наблюдатель воспринимает звук
от двух камертонов, один из которых приближается,
а другой с той же скоростью удаляется. При этом
наблюдатель слышит биения с частотой n
= 2 Гц. Найти скорость каждого камертона, если
частота их колебаний ![]() о =
680 Гц и скорость звука с = 310 м/с.
о =
680 Гц и скорость звука с = 310 м/с.
25. Струна массы М закреплена с обоих концов. В
ней возбудили колебания основного тона с
круговой частотой ![]() и
максимальной амплитудой смещения А0. Найти
максимальную кинетическую энергию струны.
и
максимальной амплитудой смещения А0. Найти
максимальную кинетическую энергию струны.