Задачи по молекулярной физике

1. Температура гелия (молярная масса = 4 г/моль), распределение молекул которого по скоростям можно считать максвелловским, изменилась от Т₁ = 200 К до Т₂ = 400 К. Число молекул, скорости которых лежат в интервале скоростей от V до V + V, осталось прежним. Определить скорость этих молекул.

2. Полагая распределение молекул азота (молярная масса = 28 г/моль) по скоростям максвелловским, рассчитать наивероятнейшую скорость поступательного движения одной молекулы и среднюю полную энергию всех молекул, занимающих при давлении Р = 2*10⁵ Па и температуре t = 27°С объем V = 30 литров.

3. Идеальный газ (гелий), имеющий температуру Т, находится внутри цилиндра высоты Н и радиуса r₀. Газ вместе с цилиндром вращается вокруг оси цилиндра с угловой скоростью . Во сколько раз концентрация молекул у стенок цилиндра превосходит их концентрацию на расстоянии г = r₀/2 от оси цилиндра?

4. Оценить радиус г мелких шарообразных частичек вещества, взвешенных в жидкости, если при увеличении высоты на h = 13*10^-3 мм концентрация частичек вещества уменьшается в = 2 раза. Температура жидкости t = 27°С, плотность жидкости r ₁ = 0,9*10³ кг/м³, плотность вещества частичек r ₂ = 1,2*10³ кг/м³.

5. Сосуд, содержащий одноатомный идеальный газ (молярная масс; = 4 г/моль), движется со скоростью U = 100 км/час. Оценить, насколько возрастут средний квадрат скорости теплового движения атомов и температура газа при остановке сосуда. Теплоемкостью и теплопроводностью стенок сосуда можно пренебречь.

6. Металлический чайник с водой нагревается на газовой плите. Вода кипит и образуется пар с постоянной скоростью выделения = 1,3*10^-2 г/с. Удельная теплота парообразования воды равна L = 2,25*10⁶ Дж/кг. Дно чайника площадью S = 0,03 м² покрыто накипью толщиной l= 1 мм. Коэффициент теплопроводности накипи = 1,25 Дж/(с*м*град). Считая теплопроводность металла, из которого изготовлен чайник, значительно больше теплопроводности накипи, оценить разность Т температур между наружной поверхностью дна чайника и поверхностью накипи, контактирующей с водой.

7. В сосуде при комнатной температуре находится смесь идеальных газов: m₁ = 4 кг одноатомного неона и m₂ = 1 кг двухатомного водорода. Определить удельную теплоемкость смеси в изохорическом процессе С_vm. Молярные массы неона и водорода равны, соответственно, ₁ = 20 г/моль, m ₂ = 2 г/моль.

8. Квазистатическое расширение идеального газа происходит по закону V = а Р^-1/2, где а = const. Определить молярную теплоемкость газа в этом процессе, если его молярная теплоемкость при изохорическом процессе известна и равна С_v.

9. Идеальный газ находится в сосуде объемом V₁ под давлением P₁. Затем газ сжимают до объема V₂ = V₁/2 так, что его давление изменяется по закону Р ~ 1/V². Определить работу газа в этом процессе.

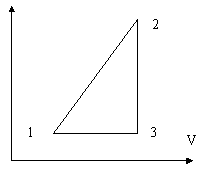10. Определить коэффициент полезного действия тепловой машины, использующей в качестве рабочего тела идеальный одноатомный газ и работающей по обратимому циклу, представленному на рисунке. Объемы и отношение температур в 1-ом и 2-ом состояниях равны, соответственно, V₁ = 5 литров, V₂ = 10 литров, Т₂/T₁ = = 2,5.

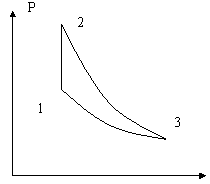11. Тепловая машина с идеальным газом в качестве рабочего вещества совершает обратимый цикл, состоящий из изохоры 1-2, адиабаты 2-3 и изотермы 3-1 (см. рис). Определить коэффициент полезного действия h данной машины, как функцию максимальной Т₂ и минимальной Т₁ температур, достигаемых в этом цикле.

12. Идеальный газ в количестве n = 2 моля изотермически сжимают от объема V₁, до объема V₂ = V₁/2. Найти изменение энтропии газа в этом процессе.

13. Теплоизолированный цилиндр разделен на две секции объемом V₀ каждая невесомым поршнем, который может передвигаться без трения. Первоначально поршень закреплен, в одной секции цилиндра находится 1 моль идеального газа, а другая пуста. Затем поршень получает возможность свободно перемещаться, и происходит самопроизвольное необратимое расширение газа. Определить изменение температуры и энтропии после установления равновесного состояния.

14. Одинаковое количество молей ₁ = ₂ = = 50 молей водорода и кислорода находятся в разных сосудах, имеющих одинаковые объемы V₁ = V₂ = V = 20 литров. Оба газа подчиняются уравнению Ван-дер-Ваальса, в котором постоянные а для водорода и кислорода равны, соответственно, а₁(Н₂) = 0,024 [м⁶*Па/моль²], а₂{О₂) = 0,14 [м⁶* Па/моль²], а постоянные b можно считать одинаковыми b₁ = b₂. Определить, насколько будут отличаться давления на стенки сосудов, содержащих водород и кислород.

15. Капилляр с запаянным верхним концом, внутренние г = 0,44 мкм и длиной l = 30 см вертикально опускают в широкий сосуд с жидкостью так, что этот капилляр оказывается погруженным на половину своей длины. При этом жидкость поднимается в капилляре на высоту h. = 1/4 над ее уровнем в сосуде. Жидкость полностью смачивает стенки капилляра, ее плотность равна = 1,26 г/см³. Атмосферное давление P_A = 10⁵ Па. Определить коэффициент поверхностного натяжения s жидкости.

16. Определить теплоемкость идеального газа в процессе: P²V = const.

17. Пусть ₀ - отношение концентрации молекул водорода к концентрации молекул азота вблизи поверхности Земли, a - соответствующее отношение на высоте h = 3000 м. Найти отношение /₀ при Т = 280 К, полагая, что температура и ускорение свободного падения не зависят от высоты. R = 8,3 Дж/моль*К.

18. Молекулы идеального газа, у которого = 1,40 и давление P = 100 кПа, имеют среднюю энергию <> = 2,5*10^-20 Дж. Найти число молекул в единице объема.

19. Вычислите количество теплоты, которое надо сообщить молю двухатомного идеального газа при его изобарическом обратимом нагревании, если а процессе нагрева газ совершил внешнюю работу в 20 Дж.

20. При какой температуре газа, состоящего из смеси азота и кислорода, среднеквадратичные скорости молекул азота и кислорода будут отличаться друг от друга на V = 30 м/с? Постоянная Больцмана k = 1,38*10^-23 Дж/К.

21. Вычислить долю молекул идеального газа, имеющих модуль скорости в интервале от нуля до наивероятнейшей скорости.

22. Некоторая масса азота заключена в сосуде, емкость которого 2 л. Температура азота 27⁰С, давление газа на стенки сосуда P = 13,3*10^-5 Па. Определите, сколько молекул азота содержится в сосуде, массу азота в нем и внутреннюю энергию газа. R = 8,3 Дж/моль*К; = 1,4.

23. В сосуде, объем которого V = 5 л, находится кислород массой m = 4 г при температуре t = 13⁰С. Определите внутреннюю энергию газа и давление газа на стенки сосуда. R = 8,3 Дж/моль*К; = 1,4.

24. Найти приращение энтропии алюминиевого бруска массой m = 3,0 кг при нагревании его от T₁ = 300 К до T₂ = 600 К, если в этом интервале температур теплоемкость алюминия C = a + bT, где а = 0,77 Дж/{г*К), b = 0,46 мДж/(г*К²).

25. Гелий массой m = 1,7 г адиабатически расширили в п = 3,0 раза и затем изобарически сжали до первоначального объема. Найти приращение энтропии газа в этом процессе.

26. Идеальный газ с показателем адиабаты совершает прямой цикл, состоящий из адиабаты, изобары и изохоры. Найти КПД цикла, если при адиабатическом процессе объем идеального газа увеличивается в п раз.

27. Один моль кислорода, находившегося при температуре T₀ = 290 K, адиабатически сжали так, что его давление возросло в = 10 раз. Найти температуру газа после сжатия и работу, которая была совершена над газом.

28. Найти относительное число молекул идеального газа, скорости которых отличаются от средней не более чем на 1 %.

29. Теплоизолированный сосуд разделен перегородкой на две большие части так, что объем одной из них в п = 2,0 раза больше объема другой. В меньшей части находится ₁ = 0,30 моля азота, а в большей части ₂ = 0,70 моля кислорода. Температуры газов одинаковые. В перегородке открыли отверстие и газы перемешались. Найти приращение энтропии системы, считая газы идеальными.

30. В двух сосудах объемом V₁ = 5 л и V₂ = 7 л находится воздух под давлением P₁ = 2 атм и P₂ = 1 атм. Температура в обоих сосудах одинаковая. Какое давление установится, если сосуды соединить между собой? Температура воздуха не меняется.