Задачи по термодинамике и статистической физике

1. Для идеального газа pV = , c_V = const получить уравнение адиабаты p = p(V).
2. Для идеального газа pV = , c_V = const получить уравнения политропы p = p(V), p = p(), V = V().
3. Показать, что для идеального газа pV =  удельная теплоемкость c_p = c_V + 1.
4. Определить КПД тепловой машины, работающей по циклу, состоящему из двух изотерм
   = ₁, = ₂, пересеченных двумя адиабатами.
5. Показать, что КПД теплового двигателя не может превысить КПД цикла Карно, работающего в том же диапазоне температур.
6. Показать, что если теплоемкость твердого тела c_V = a³ + ..., то теплоемкость c_p отлична от c_V в членах разложения порядка ⁷.
7. Для идеального газа pV = , c_V = const, получить барометрическое распределение плотности в поле силы тяжести U (z) == mgz.
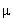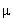8. Исходя из равновесия жидкости и газа _gas(,p) = _lq(,p), получить выражение для температурного градиента давления dp/dt насыщенного пара.
9. Полагая, что давление равновесного электромагнитного излучения равно трети плотности его энергии u = 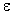/V, получить температурную зависимость u = u().
10. Считая dS = 1/(d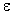 + pdV) полным дифференциалом в переменных (,V), выразить величину (d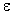/dV) через уравнение состояния p = p(,V).
11. Показать, что если теплоемкость c_V ~ ^a, то энтропия системы имеет тот же характер зависимости от температуры.
12. Указать условия, при которых равновесное состояние системы соответствует максимальному значению энтропии.
13. Указать условия, при которых равновесное состояние системы соответствует минимальному значению свободной энергии.
14. Указать условия, при которых равновесное состояние системы соответствует минимальному значению свободной энтальпии.
15. Указать условия, при которых равновесное состояние системы соответствует минимальному значению термодинамического потенциала Q = - pV.
16. Показать, что, если задана средняя энергия системы

( W_k - вероятность нахождения системы в состоянии к с энергией
_k), то энтропия системы максимальна при условии, что W_k - каноническое распределение.

17. Показать, что для равновесной классической нерелятивистской системы средняя кинетическая энергия частиц равна 3/2.
18. Вычислить свободную энергию и уравнения состояния (p = p(V,), 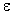=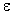()) классического идеального одноатомного газа.
19. Определить среднее число частиц идеального классического газа, падающих за секунду на 1 cm² стенки.
20. Исходя из распределения Гиббса для классической системы, показать, что

    

и привести примеры использования этих соотношений.

21. Для вырожденного ( = 0) идеального Ферми-газа определить граничные значения импульса и энергии частиц.
22. Для идеального нерелятивистского бозе-газа определить точку ₀ начала бозе-конденсации.
23. Определить среднюю энергию гармонических колебаний, происходящих в равновесных статистических системах.
24. Представляя равновесное излучение суперпозицией гармонических колебаний электромагнитного поля, определить спектральную плотность энергии .
25. Определить парамагнитную восприимчивость идеального Ферми-газа, связанную с наличием у ее частиц собственного магнитного момента.