| Численные методы в физике |
 |
1. |
Найти интерполяционные
полиномы Лагранжа 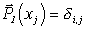 для для 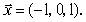 |
| 2. |
2. Найти интерполяционный полином для
функции, известной в трех точках: f(-1)=f1, f(0)=f2,
f(1)=f3. |
| 3. |
Функция задана в семи точках (x,
y):
? |
x |
y |
1 |
1 |
1 |
2 |
2 |
1 |
3 |
3 |
1 |
4 |
4 |
1 |
5 |
1 |
2 |
6 |
2 |
2 |
7 |
3 |
2 |
Какой полином P(x, y) следует использовать для
интерполяции? |
| 4. |
Для нелинейной аппроксимации
предполагается использовать функцию 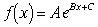 . .
Предложите способ нахождения A, B и С. |
| 5. |
Функция 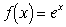 дифференцируется
по формуле: дифференцируется
по формуле: 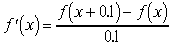 в интервале [0 .. 1]. Чему
равна максимальная погрешность
дифференцирования. в интервале [0 .. 1]. Чему
равна максимальная погрешность
дифференцирования. |
| 6. |
Получить разностную схему для третьей
производной. Функция задана на равномерной
сетке. |
| 7. |
Найти g(t), где 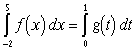 . . |
| 8. |
Предложить схему численного нахождения
интеграла 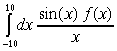 , где f(x) - функция без
особенностей. , где f(x) - функция без
особенностей. |
| 9. |
Найти полином P2(x), ортогональный
на отрезке [0 .. 1] к полиномам p0(x)=1 и p1(x)=x.
|
| 10. |
Оценить ошибку интегрирования 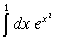 методами: методами:
а) прямоугольников;
б) трапеций;
в) Симпсона;
г) Гаусса по 3 точкам. |
| 11. |
Привести пример логической операции,
которая истинна с точки зрения традиционной
арифметики и ложна с точки зрения арифметики
конечной точности. |
| 12. |
Привести к системе уравнений 1го
порядка задачу Коши: 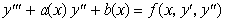 , ,
где y(x0)=y0, 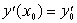 , , 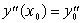 , y0, , y0, 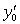 и и 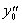 - константы.
- константы. |
| 13. |
Исследовать устойчивость уравнения 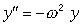 , y(0)=0 на интервале [0 .. 2 , y(0)=0 на интервале [0 .. 2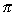 ]. ].
|
| 14. |
Уравнение 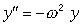 интегрируется
методом Эйлера на интервале [0 .. 1]. Какой выбрать
шаг, чтобы точность нахождения y была не хуже 10-4? интегрируется
методом Эйлера на интервале [0 .. 1]. Какой выбрать
шаг, чтобы точность нахождения y была не хуже 10-4?
|
| 15. |
Записать в общем виде уравнение Рунге -
Кутта 6го порядка. |
| 16. |
Свести дифференциальное уравнение 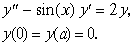
к алгебраической (матричной) задаче на
собственные значения. |
| 17. |
Дано: 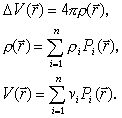
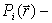 известные функции, i и vi-
набор констант. Составить систему уравнений для
нахождения I. известные функции, i и vi-
набор констант. Составить систему уравнений для
нахождения I.
|
| 18. |
Расписать один шаг метода Коуэлла
(неявная многошаговая схема) для уравнения y' =
f(x,y). |
| 19. |
Свести задачу на собственные значения y" = y,
y(0)=y(a)=0.
к многократному решению задачи Коши (метод
"стрельбы"). |
| 20. |
Записать словами или на языке
программирования PASCAL или СI алгоритм
автоматического выбора шага при интегрировании
дифференциального уравнения y' = f(x, y(x)) методом
Рунге - Кутта. |
![]() .
. 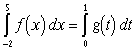 .
. 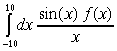 , где f(x) - функция без
особенностей.
, где f(x) - функция без
особенностей. 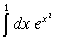 методами:
методами: ![]() ,
, ![]() ,
, ![]() , y0,
, y0, ![]() и
и ![]() - константы.
- константы.![]()
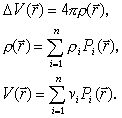
![]() известные функции, i и vi-
набор констант. Составить систему уравнений для
нахождения I.
известные функции, i и vi-
набор констант. Составить систему уравнений для
нахождения I.