Радиоэлектроника
|
 |
1. |
RC-фильтр состоит из цепочки трёх
одинаковых интегрирующих звеньев. При каком
значении функции передачи по напряжению и на
какой частоте фильтр повернёт фазу на ,если R=10
kOм, С=10 нФ? |
| 2. |
К генератору с выходным сопротивлением R0
=60 Ом подключён последовательный
колебательный контур L=0.05 Гн, C=200 пФ, R=60
Ом. Во сколько раз напряжение на индуктивности
превышает при резонансе выходное напряжение
генератора? Как изменится добротность контура,
если параллельно индуктивности включить
нагрузочное сопротивление RH=100 Ом?
Изменится ли при этом собственная частота
контура ? |
| 3. |
Определить максимально возможный
"коэффициент полезного действия"
двухполупериодного выпрямителя. Чему равен
коэффициент пульсаций (отношение мощности
переменной составляющей к мощности
выпрямленного напряжения),если не используется
фильтр? |
| 4. |
НЧ-усилитель собран на плоскостном
транзисторе с коэффициентом усиления =100. В
цепи коллектора стоит сопротивление R К=150
Ом, а в цепи эмиттера - 500 Ом. Какое
сопротивление необходимо поставить в цепь базы,
чтобы обеспечить линейный режим усиления?
Определите коэффициент усиления по напряжению и
входное сопротивление. |
| 5. |
Рассчитать параметры классической
схемы мультивибратора на транзисторах, если
длительность импульса Т1 = 1мс, а
длительность паузы Т2=2мс. Значение =100
- одинаковое для двух транзисторов.
Сопротивления нагрузки в цепях коллекторов - по 100
Ом. |
| 6. |
В RC-генераторе используется мостик
Вина, цепочка , состоящая из интегрирующего и
дифференцирующего RC-звеньев (R1=R2=10
кОм, C1=C2=10 нФ). По критерию
Найквиста определить минимальный коэффициент
усиления по напряжению. Определите частоту
генерируемых колебаний? |
Теория
колебаний
|
 |
1. |
Найти в классическом приближении
отношение частот колебаний для молекул H2,
HD (D-атом дейтерия) и D2. |
| 2. |
Записать систему уравнений для
осциллятора, описываемого гамильтонианом H = P2/2 + kX2/2, (k>0).
Постройте фазовый портрет и определите период
колебаний. Найдите частное решение системы
канонических уравнений для начального условия X=0
при t=0. |
| 3. |
Найти общее решение уравнения 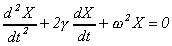 . .
Дать общую классификацию фазовых портретов.
Проанализировать решение на асимптотическую
устойчивость.
|
| 4. |
Динамическая система описывается
уравнением 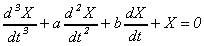 . .
Получить характеристическое уравнение. В
плоскости параметров (a,b) методом
Раусса-Гурвица построить область устойчивости.
|
| 5. |
Получить систему укороченных уравнений
для амплитуды А и фазы Ф колебаний в
генераторе Томсота, описываемого
уравнением 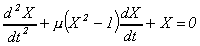 . .
Определить значение установившейся амплитуды. |
| 6. |
Релаксационный процесс описывается
системой уравнений 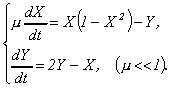
Выполнить разбиение фазовой плоскости на
траектории быстрых и медленных движений.
Исследовать особые точки траекторий на
устойчивость. |
Теория волн
|
 |
1. |
Вывести уравнение для цепочки,
состоящей из частиц с одинаковой массой.
Получить дисперсионное уравнение и построить
дисперсионную характеристику. |
| 2. |
Вывести уравнение для цепочки,
состоящей из частиц двух видов с массами m и M.
Получить дисперсионное уравнение и построить
дисперсионную характеристику. |
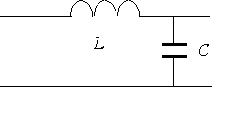
| 3. |
Вывести уравнение для цепочки состоящей
из дискретных звеньев. Получить из них уравнения
длинной линии, волновое уравнение. |
 |
| 4. |
Построить дисперсионную
характеристику цепочки 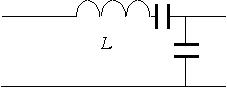
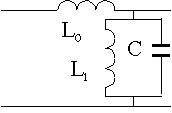
|
| 5. |
Найти спектр собственных частот
для линии длины d с эквивалентными схемами
приведёнными в задачах 3 и 4. Рассмотреть случаи: 1)
концы линий короткозамкнуты, 2) концы линии
разомкнуты. |
| 6. |
Определить зависимость
показателя преломления от частоты, считая что
оптические электроны вещества представляют
осцилляторы 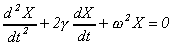
с заданной концентрацией N. |
| 7. |
Определить частоты E-мод (H-мод)
прямоугольного волновода с поперечным сечением ab
и определить напряженности E и H -полей для
этих мод. |